[L543] Diameter of Binary Tree

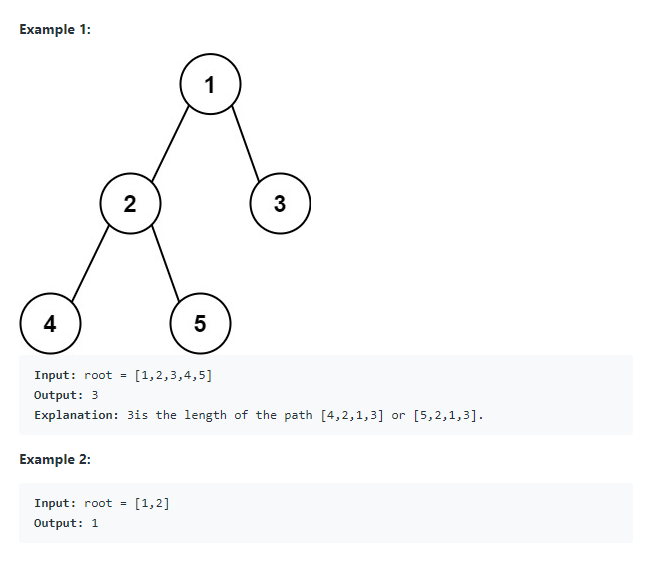
1. 문제 설명

트리의 루트 노드가 주어지면 트리의 지름을 반환하시오. (단, 트리의 지름은 두 노드 간 가장 긴 경로를 뜻한다.)

2. 제약 조건

한 트리에 있는 노드의 개수는 0개 이상 $10^4$ 개 이하다.
노드의 값은 $-100$ 이상 $100$ 이하다.

3. 접근

트리의 지름은 정의상 어떤 리프 노드에서 다른 리프 노드까지의 경로일 수밖에 없다. 만약 어떤 지름이 리프 노드가 아닌 노드를 포함하고 있다면, 리프 노드를 선택할 경우 언제나 거리가 늘어나기 때문에 모순이 발생하기 때문이다.

또한, 트리의 지름은 반드시 어떤 서브 트리의 루트 노드를 지나야 한다. 그 루트 노드가 트리 전체의 루트 노드일 필요는 없지만, 한 리프 노드가 다른 리프 노드와 만나기 위해서는 루트 노드를 지나는 것이 필연적이기 때문이다.

따라서 트리의 모든 노드를 루트 노드라고 가정하고 왼쪽과 오른쪽 서브 트리의 최대 깊이를 구한 후, 그 합의 최댓값을 구하면 트리의 지름을 얻을 수 있을 것이다.

정리하면, 필요한 연산은 아래와 같다.

한 노드에서 왼쪽과 오른쪽 서브 트리의 최대 깊이를 구하는 연산
1.에서 구한 최대 깊이의 전체 최댓값을 구하는 연산

4. 구현

class Solution {
public:
    
    int maxDepth = -1;
    
    int diameterOfBinaryTree(TreeNode* root) {
        
        updateMaxDepth(root);
        return maxDepth;
    
    }
    
    int updateMaxDepth(TreeNode* root){
        
        if(root == nullptr)
            return 0;
        
        int left = updateMaxDepth(root->left);
        int right = updateMaxDepth(root->right);
        
        // 전체 최댓값 갱신
        maxDepth = max(maxDepth, left + right);
        
        // 양쪽 서브 트리의 깊이 중에서 가장 큰 값 + 자기 자신(1)
        return max(left, right) + 1;
        
    }
    
};

5. 참고한 링크

포럼에서 가장 많은 업보트를 받은 코드를 참고했다.